最近在长尾问题上一个比较流行的方法是将深度学习模型的特征表示器和分类器解耦,这种两阶段的方法的缺点在于需要额外的微调阶段,将表示器和分类器分开优化可能导致次优结果;并且这种方法虽然效果很不错,但是无法解释为什么要把两个训练过程分开。
本文揭示了长尾目标检测的主要问题是正负梯度不平衡。为了解决梯度不平衡的问题,本文引入了一种新版本的均衡损失(EQL v2)。这是一种新颖的梯度引导的重新加权机制,可以独立、平等地重新平衡每个类别的训练过程。
7.1 EQL v2的思想和方法
该损失函数的思想如下。
假设我们有一批实例 I 及其表示。为了输出C个类别的logits:Z,我们使用权重矩阵W来对特征表示进行线性变换。W中的每个权重向量,我们称之为类别分类器,负责一个特定的类别,即:一个task。然后通过sigmoid函数将输出logit转换为预测概率分布P。我们期望对于每个实例,只有相应的分类器给出高分,而其他分类器给出低分。也就是说,一个训练实例对1个task来说是正例,而对其余C-1个tasks来说是负例。
因此,可以计算出对于第 j 个task来说实际的正例数和负例数分别为:
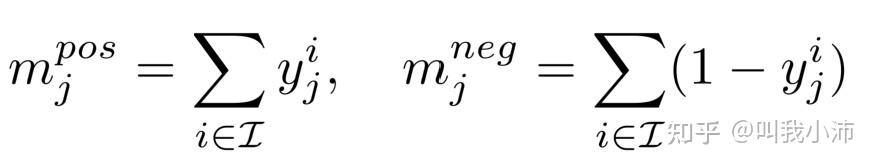
数据集上正样本和负样本的期望比率为:
虽然看起来形式很花里胡哨,实际上就是$m^{pos}_j$和$m^{neg}_j$的比值。
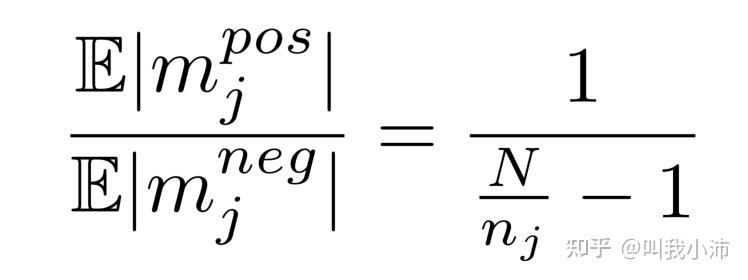
其中$n_j$是类别$j$所含有的实例数;$N$是数据集中的实例总数。
每个task的输出$z_j$关于损失$L$的累积正梯度和负梯度如下:
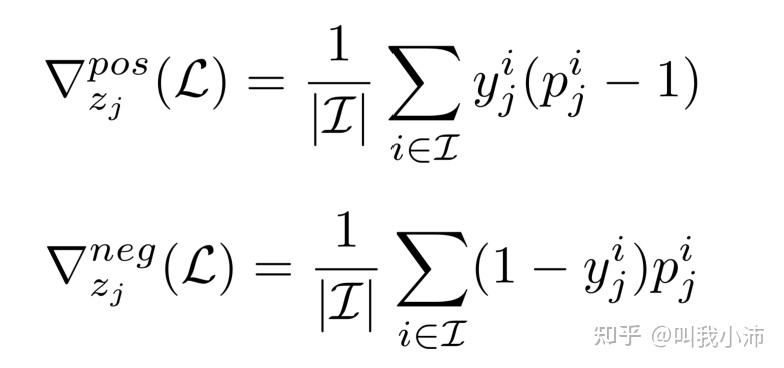
其中$p_j^i$表示第$i$个实例在第$j$类上的估计概率。
梯度引导平衡重加权的基本思想是,根据每个分类器累积的正负梯度比,分别对正梯度和负梯度进行加权和减权。
下面直接给出了公式,并没有解释为什么要这样,懵逼警告。
首先定义$g_j^{(t)}$作为第$ t $次迭代之前task $j$ 的累积正梯度与负梯度之比。下面给出了正梯度的权重$q_j^t$和负梯度的权重$r_j^t$的计算公式:
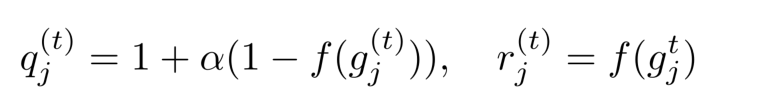
其中$f(*)$是一个映射函数:
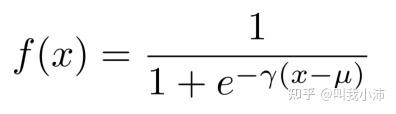
得到了$q_j^t$和$r_j^t$之后,把它们用到当前批次的正梯度和负梯度上,得到:
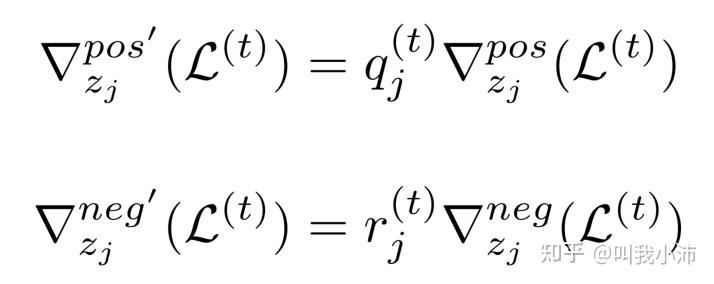
最后,更新下次迭代的累积的正梯度与负梯度之比:
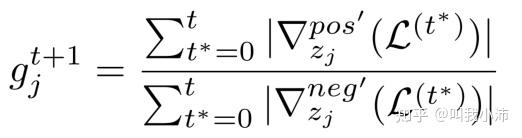
7.2 实验
在LVIS v0.5上与最新方法的比较:
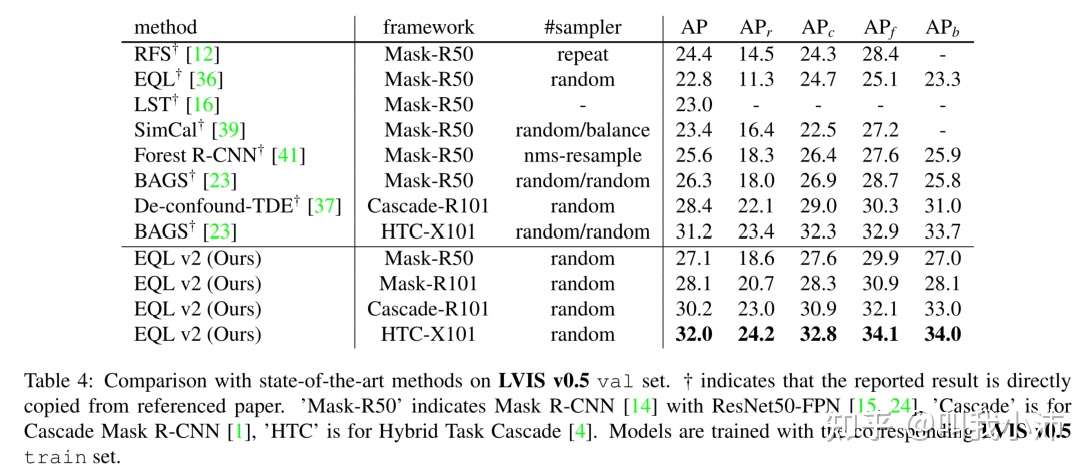
从表中可以看出,本文所提方法有一定提升;
在LVIS v1.0上与最新方法的比较:
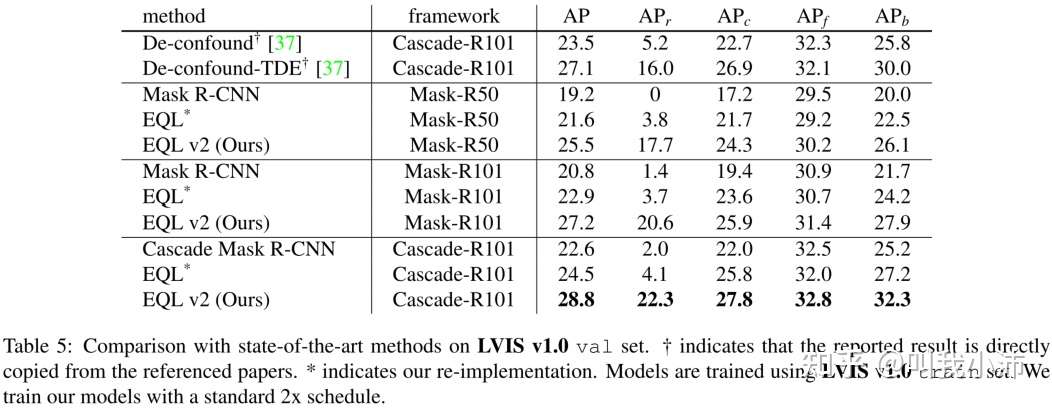
从表中可以看出,本文所提方法仍有一定提升;
存疑:这里为什么不跟BAGS比了呢?
在Open Images上的结果:
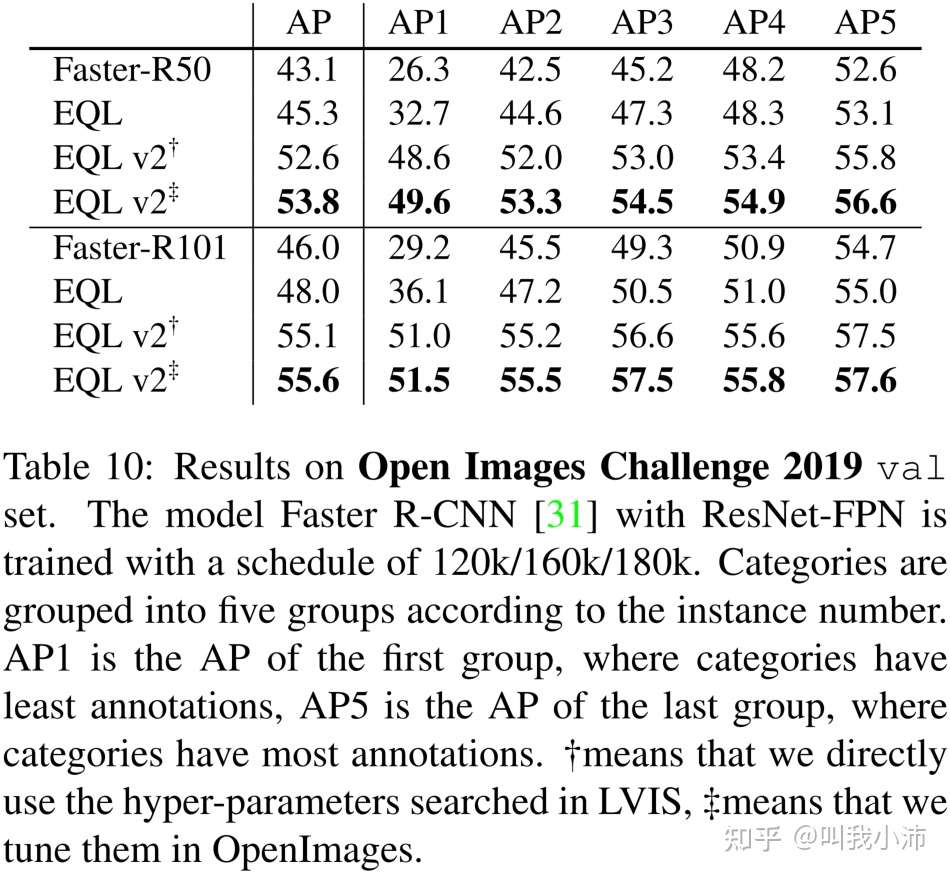
奇怪,参与对比的方法怎么越来越少了?
总结:EQL v2的整个步骤:(我的理解)
1)计算每个task的输出$z_j$关于损失$L$的累积正梯度和负梯度;
2)计算第$ t $次迭代之前task $j$ 的累积正梯度与负梯度之比$g_j^{(t)}$;
3)计算出正梯度权重$q_j^t$和负梯度权重$r_j^t$;
4)将$q_j^t$、$r_j^t$分别和累积正梯度、累积负梯度相乘得到加权后的结果;
5)更新累积正梯度与负梯度之比$g_j^{t+1}$以备下次使用;
6)重复步骤3) - 5) ;
为什么要这样做?No idea. 如果理解有错误的地方,还请帮忙指出。