这篇文章是收录在CVPR 2021的一篇关于长尾分布下的目标检测的文章。提出了一种比较简单、巧妙的损失函数,有效地提升了长尾分布下目标检测的准确度。
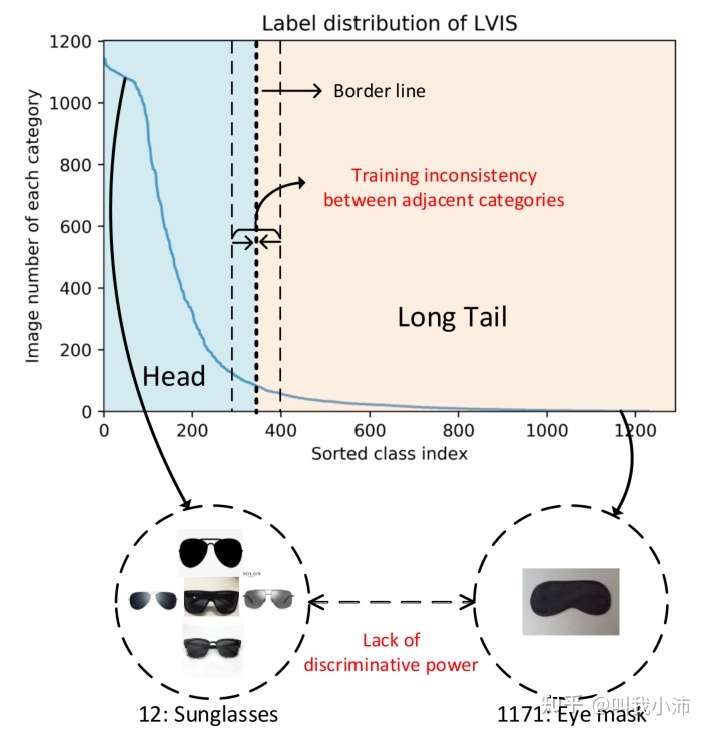
在长尾目标检测问题中,现有的方法通常是将整个数据集划分为若干组,并对每组采用不同的策略。这种方法虽然能够取得不错的结果,但是存在以下两个问题(如下图所示):
1)相似大小的相邻类别之间的训练不一致;
这种方法要通过设定一个阈值来将数据集划分为不同的组,在分界线两侧的类别虽然有相近的图片数量,但是由于被分到的组不一样而有不同的训练结果;
2)学习模型对语义上与某些头部类别相似的尾部类别缺乏区分。
因为模型是分组训练的,因此头部和尾部的相似类别可能学到的特征也非常相似,这样在最后放在一起测试时很难将两种样本区分开。
此外,分组的方法还依赖于具体数据集分布先验,当面临新的数据集分布时,这种方法需要重新调参数来确定最优的分组策略,从而限制了方法的通用性和可移植性。
6.1 分组方法的局限性验证
前面指出了现有的分组方法存在的问题,但口说无凭,下面就来实验验证,拿数据说话。
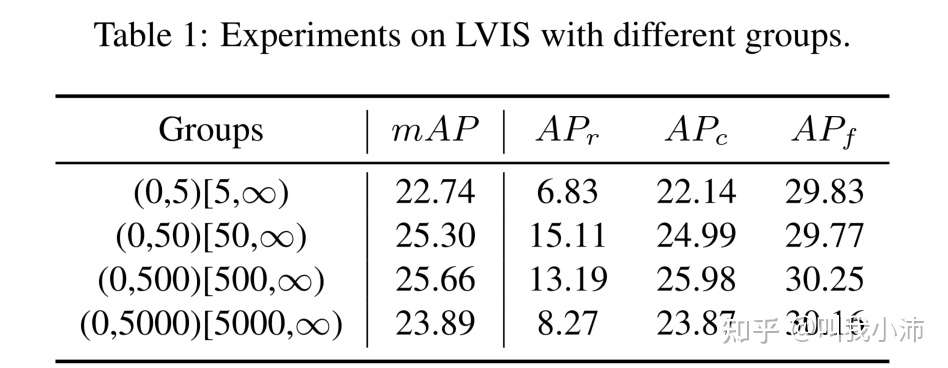
本文使用BAGS[5](一种SOTA的基于组的长尾目标检测方法)在LVIS上进行了实验,分别以5、50、500、5000为界将数据集分为两个组,得到了下面的实验结果。(下表中的r代表罕见类别,c代表常见类别,f代表频繁类别)。从表中可以看出需要设定适当的分界线(50~500),才能实现令人满意的性能,设置过大或过小都会降低性能。
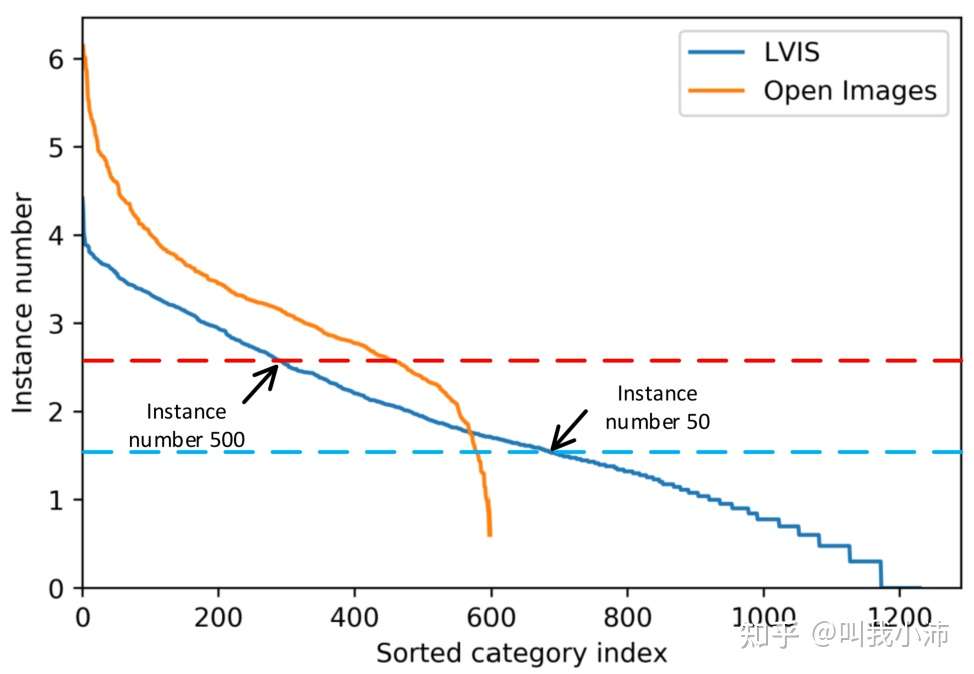
但是即便已经在一个数据集上确定了恰当的分界线,当面临不同分布的新数据集时,又需要重新确定分界线,如下图所示,我们在LVIS上确定的分界线在Open Images上并不适用。
Motivation:基于上面的讨论,很容易提出一个问题:能不能设计一种可以直接应用于不同的长尾分布数据集上的更通用的方法呢?因此本文提出了一种自适应类抑制损失(Adaptive Class Suppression Loss, 简称ACSL),可以避免上述问题。
6.2 ACSL是啥?
ACSL的思想很简单:对于数据集中的每个类别,仅保留当前类别和容易跟当前类别混淆的类别的损失,去除其余所有类别的损失。
我们先看一下多分类情况下的交叉熵损失函数:
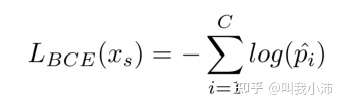
其中:
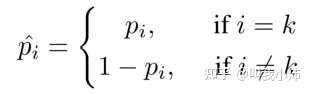
$C$ 是数据集中的类别数量。
再来看下ACSL:实际上就是在普通的交叉熵损失函数前加了个权重$w_i$:
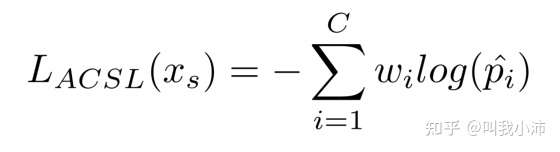
其中:
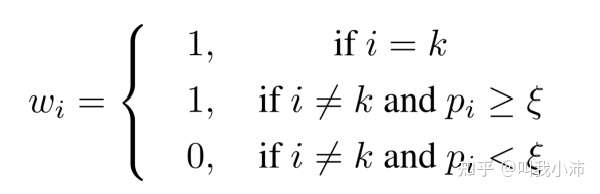
$\xi$ 是需要我们自己设定的一个阈值,范围在(0,1)之间,定义$p_i>\xi$的类别为容易混淆的类别。
这个公式(ACSL)相对于普通的交叉熵损失函数(BCE)所作的改进就是:BCE计算了所有类别的损失,而ACSL则仅计算了正确的类别和容易混淆的类别的损失,这样就“隔离”了其余类别对正确类别的影响,从而减小了头部类别在训练时对尾部类别的影响。
举个例子来说明一下:
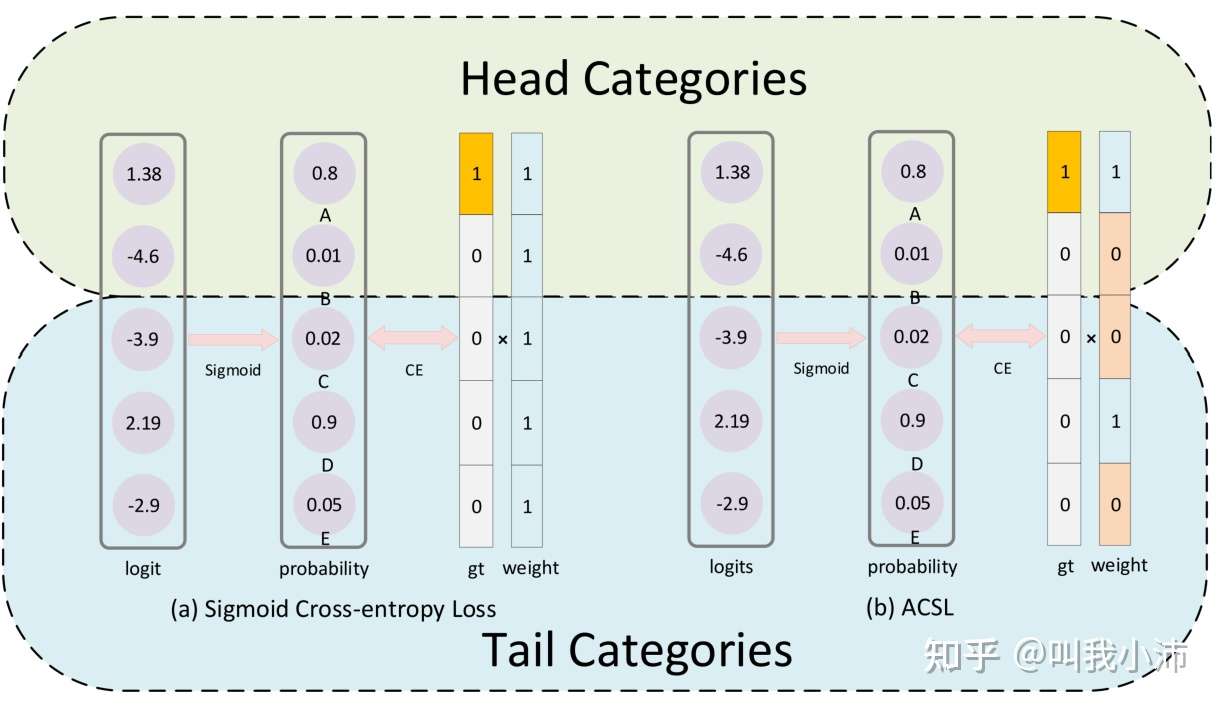
这个图表示二值交叉熵损失和ACSL对同一个样本的处理方式。该样本属于A类别,对于二值交叉熵损失来说,每个类别的损失的权重项均设置为1。对于ACSL来说,由于网络在A类别和D类别上都有比较高的得分,说明网络容易对这两个类别产生混淆,所以要保留对类别D的抑制梯度,其权重设置为1。对于类别B,C,E来说,网络产生的得分较低,所以将其对应的权重设置为0,可以避免对尾部类别产生过度的抑制作用,保护尾部类别的精度[6]。
6.3 实验结果
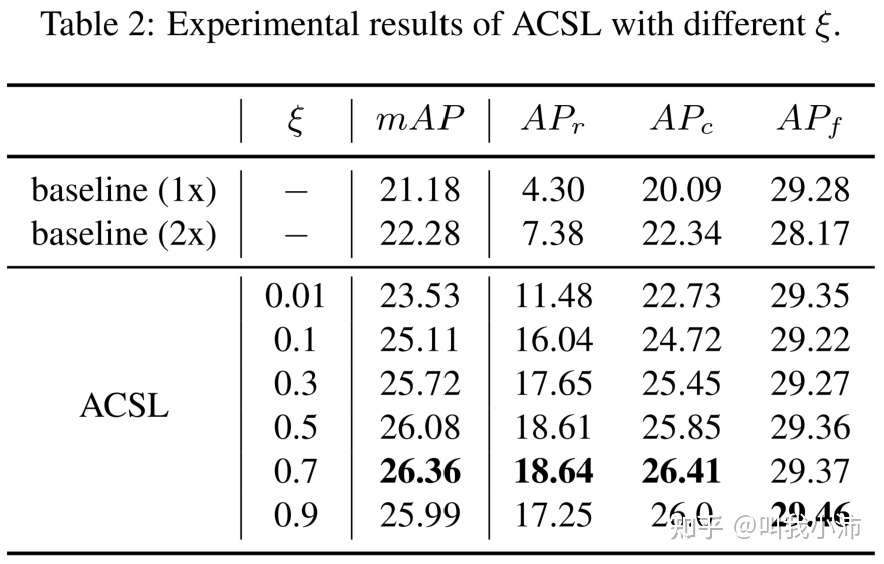
作者在LVIS数据集上进行了实验。首先进行了消融实验,对 $\xi$ 的不同取值时的检测效果进行了实验,如下表。从表中可以看出ACSL方法的检测效果较baseline有所提升,且适当增加$\xi$的值模型性能也会随之增加,当 $\xi=0.7$ 时模型达到最佳性能。
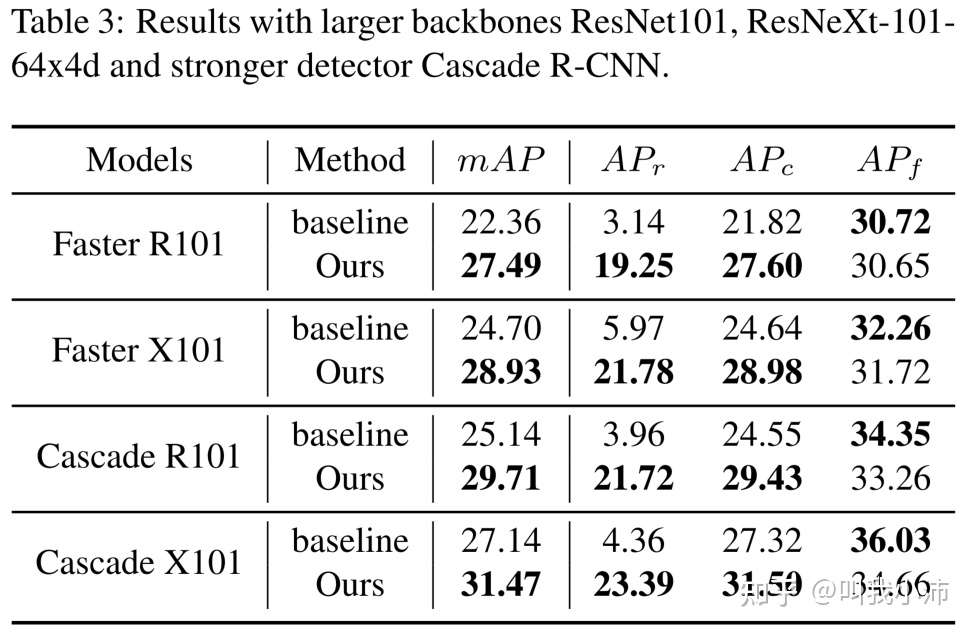
接下来验证了ACSL在不同模型上的表现都很不错(下表中的r代表罕见类别,c代表常见类别,f代表频繁类别):
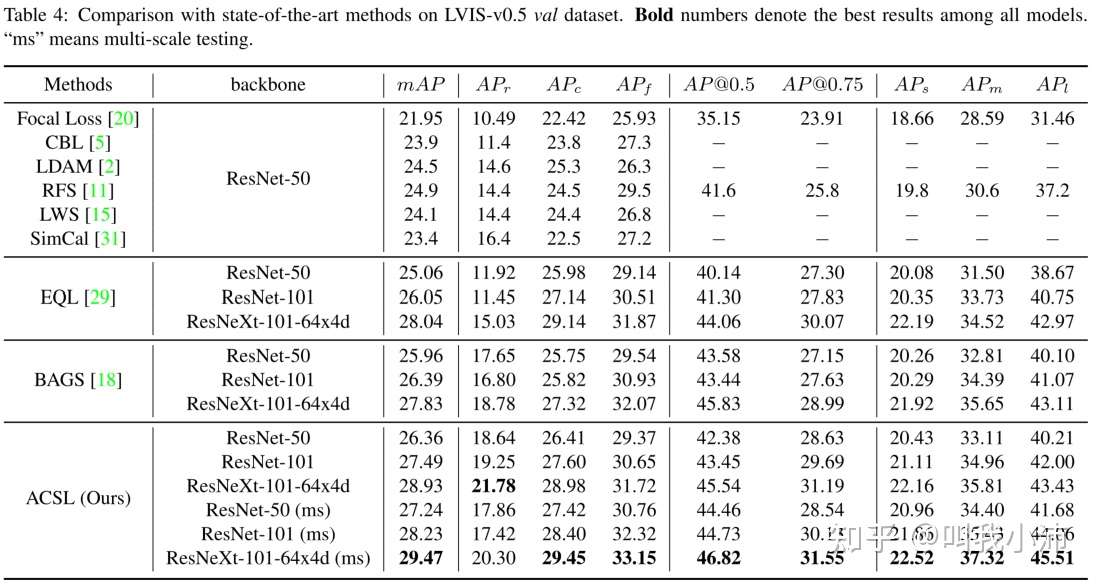
随后在LVIS-v0.5上对ACSL和以前的SOTA方法进行了对比:
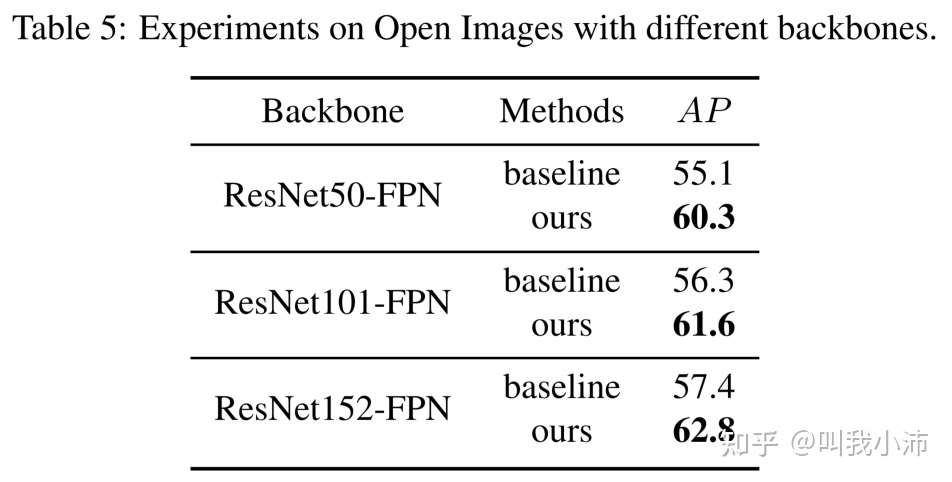
最后在最大的Open Images数据集上进行了实验,验证了本文所提方法的有效性: